orals 5th Asia-Pacific NMR Symposium 2013

Half a dozen ways to compute restricted diffusion propagators: Are some better than others? (#100)

Konstantin I. Momot 1 , Sean K. Powell 1
  1. Queensland University of Technology, Brisbane, Qld, Australia

Restricted diffusion is a well-established tool for NMR structural characterisation of sedimentary rocks, biological tissues and other multicompartment systems.1,2,3 Their morphology can be inferred from NMR diffusion-diffraction plots or the time-dependence of the apparent diffusion coefficient. These provide, respectively, the characteristic pore size and the degree of obstruction to diffusion presented by walls or cell membranes. Diffusion NMR signal attenuation can be computed from the restricted diffusion propagator, which describes the distribution of diffusing particles for a given starting position and diffusion time.

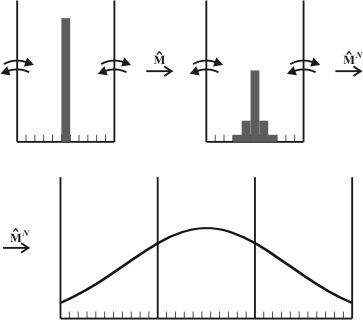
We present two novel techniques for efficient evaluation of restricted diffusion propagators for use in NMR porous-media characterisation. The first is the Lattice Path Count (LPC).4 Its physical essence is that the restricted diffusion propagator connecting points A and B in time t is proportional to the number of distinct length-t paths from A to B. By using a discrete lattice, the number of such paths can be counted exactly. The use of arbitrary-length integers enables implementation of LPC for large lattices.

The second technique is the Markov transition matrix (MTM).5 The matrix represents the probabilities of jumps between every pair of lattice nodes within a single timestep. The propagator for an arbitrary diffusion time can be calculated as the appropriate matrix power. For periodic geometries, the transition matrix needs to be defined only for a single unit cell. This means that the physical size of the system amenable to simulation is almost unlimited, making MTM ideally suited for periodic boundary conditions.

LPC and MTM perform very favourably compared to Monte Carlo sampling: they yield highly accurate and almost noiseless restricted diffusion propagators. Both new methods are applicable to complicated pore-space geometries for which no analytic solution is available. We discuss the new methods in the context of NMR techniques for characterisation of materials and tissues.

1151-Figure_Abstract_30pc.jpg

  1. PT Callaghan, A Coy et al, Nature 351 (1991) 467-9.
  2. PN Sen, Concepts Magn. Reson. 23A (2004) 1-21.
  3. SK Powell and KI Momot, Phys. Rev. E 86 (2012) 031917
  4. SK Powell, GJ Oberman and KI Momot, "Efficient calculation of restricted diffusion propagators using lattice path counts". Phys. Rev. Lett., submitted.
  5. KI Momot, "Calculation of restricted diffusion propagators using Markov transition matrices". Manuscript in preparation.